时闪闪,宇振盛
(上海理工大学 理学院,上海 200093)
本文考虑如下复合函数优化问题

式中:f:Rn→R 是连续可微函数;
g:Rn→R 是凸的非光滑函数;
可行集Ω={x∈Rn:aiTx=bi,i∈ME,aiTx≥bi,i∈MI},ME={1,···,m},MI={m+1,···,p},ai∈Rn,bi∈R,i=1,···,p。
从现实生活中的问题抽象出来的数学模型,可以分为光滑和非光滑两大类。对于光滑问题,由于其梯度及Hessian 矩阵易于求出,可以使用经典的优化算法求解。而对非光滑问题,函数是不可微的,因此无法直接使用经典的优化算法求解。此外,非光滑复合函数的极小化问题在信息理论[1]、无线通信[2-4]、图像恢复[5-7]、信号处理[8-9]、变量选择[4,10]等领域都有广泛的应用。
当可行集 Ω=Rn时,问题(1)就是无约束优化问题。目前,已经有很多学者提出了各种非常有效的算法[11-18]解决无约束复合函数问题。比较成熟的算法有迭代收缩阈值算法[12-13]、临近牛顿法[14]、分裂算法[15-16]、邻近点算法[17-18]等。
实际生活中的很多问题都要求满足一些特定的条件,所以研究带约束的复合函数问题十分有必要。例如,压缩感知理论中的稀疏信号重构问题就是经典的复合函数优化问题。稀疏重构主要解决这两类问题:在对非负信号处理时,有非负约束的限制;
进行图像恢复时,灰度强度取值在0~255 之间。在信号恢复、图像恢复模型里加入约束,可以提高恢复的准确率。同样地,对于实际问题,考虑约束限制,能更加精确地求出符合实际条件的解,从而节约成本。
当可行集 Ω={l≤x≤u}时,问题(1)就是界约束的复合函数问题。Bian 等[6]提出光滑二次正则化方法,用SQR 表示解决图像恢复中出现的界约束非Lipschitz 连续优化问题。有效集方法是求解约束优化问题的常用方法,采用有效集策略,可以加快算法的收敛速度。张涛[19]提出了一种求解界约束优化问题的新积极集信赖域算法。
生产生活中的大多数问题,往往具有更加复杂的约束,因此研究复杂约束的复合函数优化问题更具有现实意义。当可行集 Ω为多面体约束时,问题(1)就是多面体约束复合函数优化问题。简单约束复合函数优化问题的理论已经发展得十分成熟,但是关于多面体约束的复合函数优化问题,研究工作仍处于基础阶段,还有很多问题尚未解决。Liu 等[4]提出了光滑序列二次规划框架(SSQP)求解一类多面体上复合函数Lq极小化问题。实际上,有效集方法已成功地应用于大规模的线性约束光滑优化问题的求解。William 等[20]提出了求解多面体约束优化问题的新的有效集算法(PASA)。Zhang 等[1]提出了求解线性约束非凸非Lipschitz 优化的光滑有效集算法(SASA),且用于求解简单约束非光滑复合函数优化问题效果良好,即

也就是本文实际求解的模型:

它是Liu 等[4]在求解一类多面体上复合函数Lq极小化问题中求解的模型。
以上算法在求解大多数问题时表现良好,但它们不能很好地解决一般多面体约束复合函数问题,例如,SQR 算法[6]不能求解问题中f(x)的复合项Lq和一般多面体约束问题。SSQP 算法[4]的目标函数不具一般性,且由于投影收缩算法是不精确求解子问题,这会使得算法收敛速度慢。PASA 算法[20]需要求解投影梯度信息,SASA算法[1]对线性约束优化器有特殊条件限制,这两种算法都是两阶段算法,程序实现难度较大。
序列二次规划(sequential quadratic programming,SQP)是求解非线性约束优化问题的主要方法之一,它在求解中等规模和小规模的非线性问题[21-22]中表现不俗。有效集算法 (active set algorithm,ASA)在求解不等式约束优化问题时十分有效,通过有效集策略,每次只需求解仅含等式约束的优化问题,从而可以降低维度,达到提高算法收敛速度的目的。
本文提出了将ASA 和SQP 结合的新算法,该算法主要借鉴文献[4]中提到的求解多面体上最小化复合函数的光滑近似技巧及SSQP 框架,将非光滑目标函数转化成光滑函数,并利用有效集策略求解二次规划子问题。
定义1[23]函数:Rn×R+→R 称为非光滑函数g:Rn→R 的近似光滑函数,若 ∀μ>0,是连续可微的,且对 ∀μ∈Rn,有=g(x)。
非光滑优化问题的光滑近似已经得到了广泛的应用[23-24]。本文对绝对值函数
θ(t)=|t|
构造光滑函数[25]:


则式(5)是问题(1)的光滑近似函数。
不难得到 θμ(t,μ)具有的特殊性质。显然地,对任意固定的 μ>0,有
θμ(t,μ)=θ(t),∀t≥μ
和
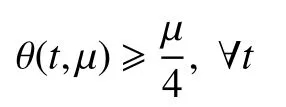
此外,θq(t,μ)是连续可微的。除在t=和t=外,θq(t,μ)在其他处都是二次连续可微的。θq(t,μ)关于t的一阶导数和二阶导数分别为

接下来,给出一个非常重要的引理。
引理1对 ∀q∈(0,1),μ∈(0,+∞),

引理1 的详细证明参见文献[4]中的引理 4.1。
本文受文献[4]的启发,采用该文献中的SSQP框架,提出了序列有效集算法(SQP-ASA),在每一迭代步中利用有效集策略求解一个凸二次规划(QP)子问题。此QP 子问题的目标函数是问题(1)光滑近似后式(5)的目标函数的局部上界。光滑参数的更新依赖于问题(1)的残差。
对固定的光滑参数 μ>0,定义非光滑函数g(·)的光滑近似函数在xk处的二次近似为
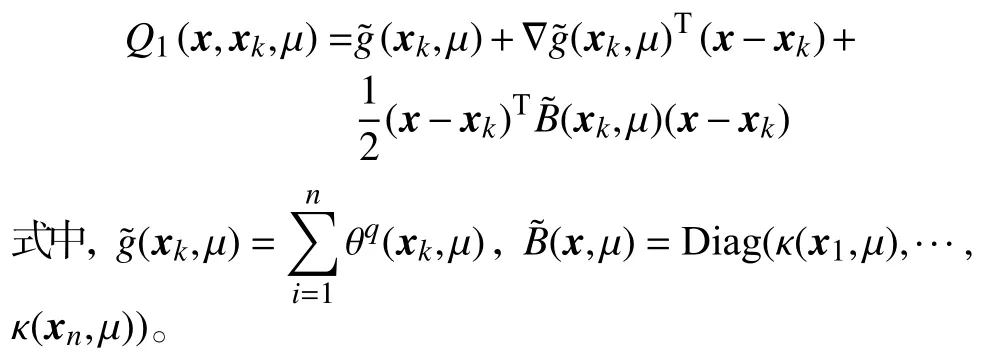
类似地,定义光滑函数f(x)在xk处的二次近似为

假设f(x)的梯度是Lipschitz 连续的,即
‖∇f(x)-∇f(y)‖2≤L‖x-y‖2,∀x,y∈Ω
定义
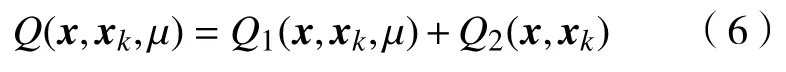
由于Q1(x,xk,μ)和Q2(x,xk)分别是和f(x)在xk处的二次近似,因此,可以把Q1(x,xk,μ)看作是在xk处的二次近似。
下面的引理给出了凸二次规划(6)的目标函数Q(x,xk,μ)是式(5)的目标函数之间的大小关系,即Q(x,xk,μ)是在xk处的一个上界,这保证了问题(6)的最小值是问题(5)最小值的上界。
引理2对任意的xk,x,使得

该引理的证明可参考文献[4]中的引理 4.2。
基于引理2,提出序列有效集二次规划算法。
本文研究的问题(2)光滑后可以表示为
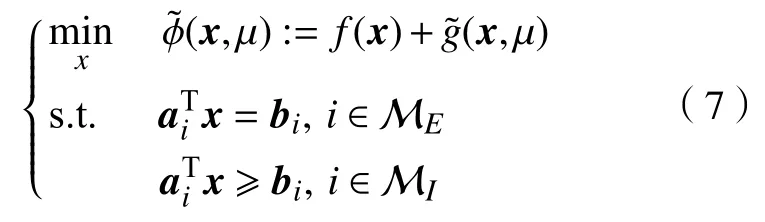
那么,问题(7)在xk处的QP 子问题为
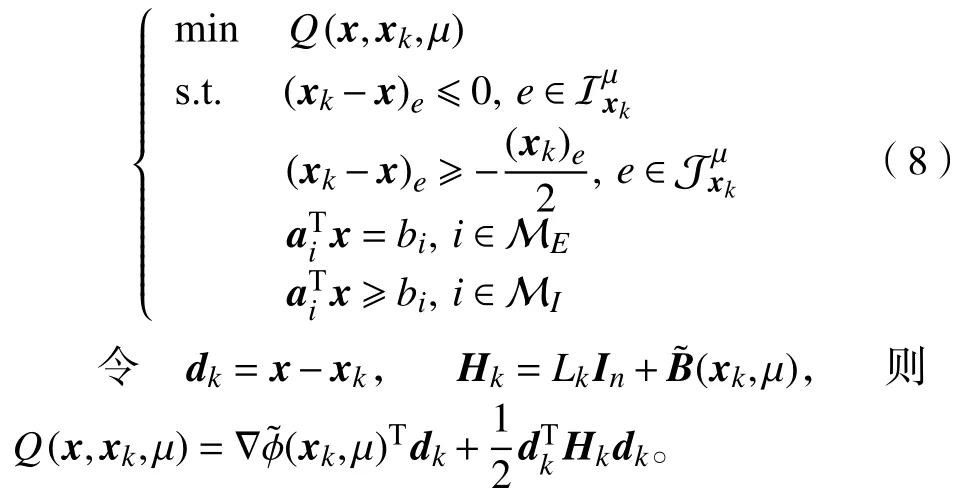
求解问题(7)的算法思想为:在每一迭代步中,首先使用有效集方法求出其二次规划子问题(8)的最优解d*,并将它作为问题(7)下一步的搜索方向dk,再利用价值函数通过Armijo 线搜索求出步长 αk,进而得到问题(7)的下一步迭代点xk+1,重复这一过程,直到求得问题(7)的最优解x*。具体求解过程如算法1 所示。

令x-xk=d,则可将QP 子问题(8)转化与d有关的子问题求解。通过积极集策略,会有越来越多的xk逐渐满足=bi,i∈Sk。这样问题就转化为了等式约束优化问题,再利用拉格朗日乘子算法对其进行求解。因此,本文的算法可以在大大减少问题维数的同时提高计算的效率。
接下来,利用文献[26]中的有效集方法求解QP 子问题,如算法2 所示。


此处的价值函数 ψ(x,μ,ϑ)=。这是因为由有效集方法得到的方向dk一定是可行方向。
为证明算法1 的全局收敛,现给出如下基本假设:
假设1对 ∀x∈Ω,线性独立约束限定 (LICQ)成立,即梯度ai(i∈Sk)线性无关。
由Hk的构造可知,Hk一定是对称正定的。本文提出的SQP-ASA 算法通过求解如下形式的二次规划问题
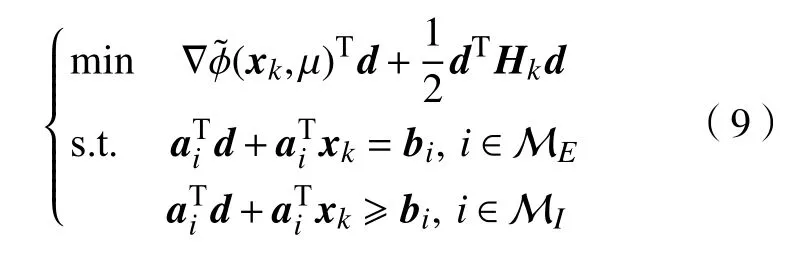
得到解d*,作为原问题变量x在第k次迭代过程中的搜索方向dk。在求解过程中利用有效集策略,通过逐次求解仅含带等式约束的相关二次规划问题(9)来逼近其最优解。
下面证明SQP-ASA 算法的全局收敛性,即证该算法产生的点列 {xk}的任何聚点x*都是问题(7)的KT点。
引理3由算法2 中的有效集方法求得的QP子问题方向dk一定是原问题(7)的可行下降方向。


因此,dk一定是原问题(7)的可行方向。
其次,证明方向dk是下降的。对 ∀μ∈(0,1],利用QP 子问题(9)的KT条件,有
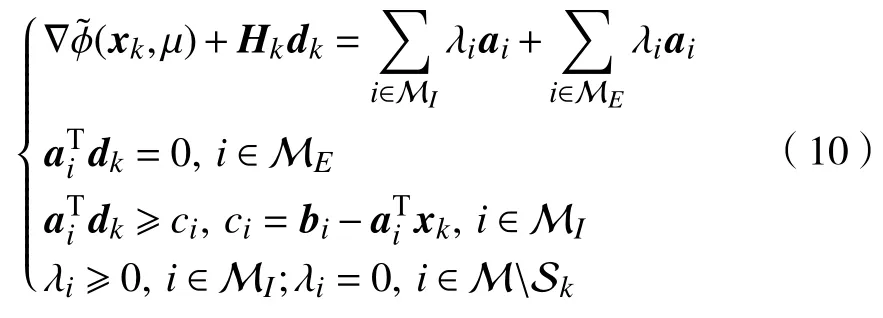
由式(10)的第一个式子可得

引理4对于上述二次规划子问题(9),设其KT点对为。如果d(x)=0,则x为问题(7)的KT点。
证明不妨设
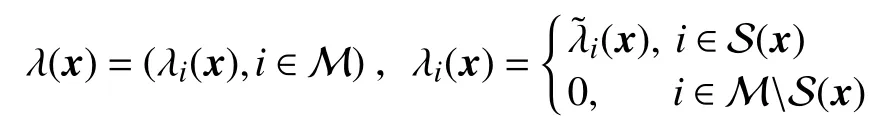
如果d(x)=0,依据有效集方法求解方向d(x)的过程,结合问题(7)的KT条件可知,≥0,否则,d(x)不是二次规划问题(9)的最优解,与KT点对这个条件相矛盾。因此
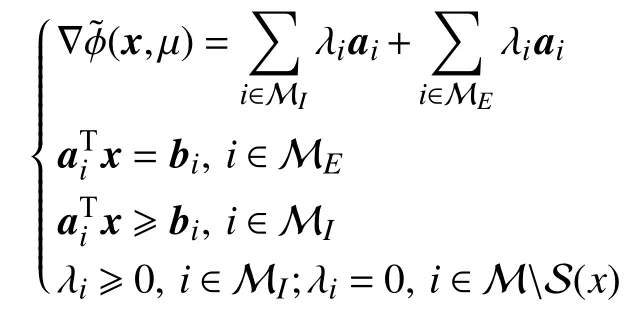
这说明x是问题(7)的一个KT点。
定理1由序列有效集算法生成的序列{xk}的任何聚点x*都是原问题的KT点。
证明对 ∀μ∈(0,1],当该算法是有限步终止时,由引理4 可知,算法产生的点列{xk}的任何聚点x*都是问题(7)的KT点。
下设该算法产生无穷点列{xk},x*为其任一给定聚点。由于 Sk∈M为有限集,不妨设存在无穷子集K,使xk→x*,Sk≡S,k∈K。为不失一般性,不妨设由SQP-ASA 算法产生的迭代点xk+1=xk+βkdk(∀k∈K),而由引理3 可知,单调下降,从而由xk→x*,k∈K可以得到,k→∞。
一方面,由于步长 β是由Armijo 线搜索得到的,所以 β∈(0,1]。另一方面,通过引理3 知dk是下降方向,不难得到
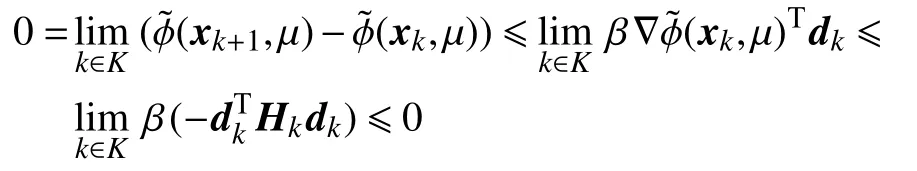
故可知dk→0,k∈K。从而-bi=0,i∈S,S⊆M(x*)。那么

这说明x*是问题(7)的一个KT点。
利用Matlab R2016a 实现算法SQP-ASA。其中试验环境为:Intel(R)Core(TM)i5-5200U CPU@2.20GHz 4.00GB RAM。通过求解下列问题的稀疏解来检验算法的有效性。
例 1非负箱约束稀疏信号恢复的模型如下

寻求该模型的稀疏解,可以转化为求解模型:
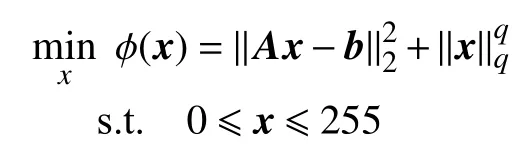
分别运用本文提出的序列有效集算法(SQPASA)和文献[4]中的序列投影收缩算法(SQPPG),求出该模型的稀疏解。相关参数取法如下:μ0=0.1,σ2=0.000 1,A=randi([-10,,10],50,50),b=randi([-10,10],50,1),L0=,Lmax=3 000,Lmin=1 137.5,精度参数 ϵ=10-5,初始点d0=254×randi([0,1],50,1),最大迭代次数为1 000。目标函数与迭代次数的关系如图1 所示。

图1 迭代次数比较Fig.1 Comparison of iteration times
这两种方法的迭代次数和迭代时间的比较见表1。从表1 可以看出,对于同样的初始点,SQPASA 算法比SQP-PG 算法的迭代次数少,运行效率也更高。

表1 例1 的数值结果Tab.1 Numerical results of example 1
例 2寻求如下函数

的稀疏解。可以转化为求解模型

本文通过求解以下两个模型在不同约束条件下的稀疏解,来验证算法的有效性。两个模型均来自文献[26]。
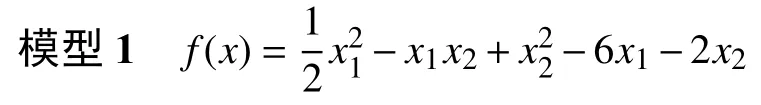

分别使用SQP-ASA 算法和SQP-PG 算法,求出该模型的稀疏解。这里的相关参数取法如下:μ0=0.01,ξ=0.5,σ=0.1,η=1.2,Lmax=20,Lmin=3,L0=3,精度参数 ϵ=10-5,初始d0=[0.5-1]T,最大迭代次数为1 000。迭代过程如图2 所示。

图2 迭代次数比较Fig.2 Comparison of iteration times
这两种方法的迭代次数和迭代时间的比较见表2。从表2 可以看出,对于同样的初始点,SQP-ASA 算法比SQP-PG 算法的迭代次数少,运行效率也更高。


表2 模型1 的数值结果Tab.2 Numerical results of model 1

分别使用SQP-ASA 算法和SQP-PG 算法,求出该模型的稀疏解。此时的相关参数取法如下:μ0=0.01,ξ=0.5,σ=0.1,η=1.2,Lmax=20,Lmin=2.181,L0=2.618,精度参数 ϵ=10-5,初始d0=[0-3]T,最大迭代次数为1 000。目标函数与迭代次数的关系如图3 所示。

图3 迭代次数比较Fig.3 Comparison of iteration times
这两种方法的迭代次数和迭代时间的比较见表3。从表3 可以看出,对于同样的初始点,SQPASA 算法比SQP-PG 算法的迭代次数少,运行效率也更高。

表3 模型2 的数值结果Tab.3 Numerical results of model 2
提出了一种新的求解多面体约束非光滑复合函数优化问题的序列有效集算法。首先,将非光滑目标函数转化为光滑目标函数;
然后,在每一迭代步中用有效集方法求解一个二次规划子问题得到方向,利用价值函数通过线搜索取得步长,重复这一过程直到求得原问题的解;
最后,证明了该算法的全局收敛性。此外,通过实例进行了数值验证,结果表明,该方法较序列投影收缩方法具有一定优势。

